
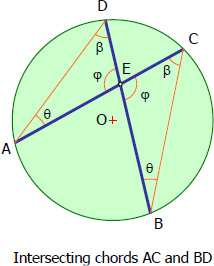
These radii each intersect on point on the. These segments form the central angles of chords AB and CD: AOB and COD, respectively. We define the arc angle to be the measure of the central angle which.
ARCS CHORDS AND CENTRAL ANGLES HOW TO
Students will learn how to identify the arcs chords and central angles in a circle as well as use theorems. A central angle of a circle is an angle formed by any two radii of the circle. An inscribed angle is an angle formed by two chords in a circle which have a common.
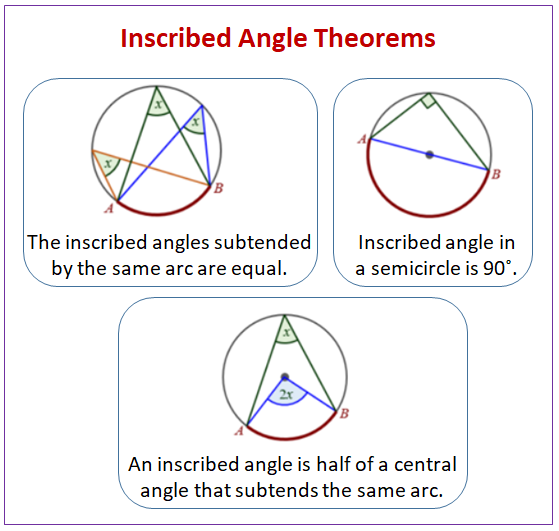
So, Īrcs, in the same circle or in congruent circles, that have equal measures 45° 45° and are in the same circle and m = m = 45°. This is a 2 flap interactive notebook foldable. 40° 80° 110°ĩ Congruent arcs and are in the same circle and m = m = 45°. What appears to be true about the arcs these angles intercept, CD and LK B. Look at the congruent central angles, CAD and LAK. The measure of the arc formed by two adjacent arcs is the sum of the measures of these two arcs. Central angles, chords, and arcs Get the Gizmo ready: Be sure One circle is selected under Figure type and Congruent central angles is selected under Conditions.
2 Objectives At the completion of the lesson, you will be able to…ĭefine and identify arcs and central angles in circles Calculate the measures of arcs and central angles in circlesģ Using Arcs of Circles Central Angle – an angle whose vertex is at the center of a circle Major Arc – formed by two points on a circle and its measure is greater than 180 named with 3 endpoints Minor Arc – formed by two points on a circle whose measure is less than 180 named with 2 endpoints Semicircle – an arc formed by two points on a circle whose measure is equal to 180Ĥ Example: Naming Arcs Name: B minor arcs: major arcs: semicircles:Īn acute central angle: Two congruent arcs: 60° 60° B 180°ĥ Measuring arcs Measure of an arc: equal to the measure of an arc’s central angle Minor arc: Major arc – think about it: how would I find 60° 60° B 180°Ħ A postulate m = m + m Arc Addition Postulate


 0 kommentar(er)
0 kommentar(er)
